| |
MODSTAND, HESTEKRÆFTER og GEARING
Når man fordobler hastigheden, firedobler man luftmodstanden og dermed behovet for motorkraft. Så simpelt er det, så kan du nøjes med det, så klik bare tilbage.
Vil du gerne vide mere, så kig lidt på det følgende.
Den almindelige formel for bremsekraft er
F * s = ½ * A * s * d * v2
F er bremsekraft, s er den tilbagelagte strækning, A er tværsnitsarealet, d er luftens densitet, v er hastigheden.
Vi starter med at fjerne faktoren s ved at dividere den væk på begge sider af lighedstegnet.
Denne formel tager desuden ikke hensyn til, at et legeme kan være kan være mere eller mindre heldigt udformet og dermed på nogle områder lader luften glide af uden videre modstand og på andre områder skaber større modstand. Det klares ved at indføre en formfaktor eller luftmodstandskoefficient, Cw.
Så bliver formlen:
F = ½ * Cw * A * d * vˆ2
Luftens densitet er tæt ved havets overflade 1,3 kg/m3.
Men tværsnitsarealet? Hvor stort er det? Der er kun at kigge i diverse bøger, blade og brochurer. Man kan også være heldig på nettet at finde oplysninger, som kan bruges.
Model |
Tværsnit i m 2 |
Porsche Carrera GT |
1,900 |
Ferrari 360 Modena |
1,900 |
Lister Storm LMP |
1,585 |
Bentley EXP Speed 8 LMGTP |
1,750 |
Joest Porsche 962 |
1,806 |
Mazda RX-792P GTP |
1,750 |
Porsche 917 K |
1,546 |
Man kan også være lidt kreativ. Tværsnitsarealet er bilens areal set ret forfra. og hvordan finder man så lige det? Min dovenskab tvinger mig til ikke at sky nogen anstrengelser, hvis det betyder, at jeg slipper for at lave noget. Find derfor et billede eller tegning af bilen set forfra.

Her er min assistent med racerversionen af min Jaguar, hvor jeg blot har gjort baggrunden ensfarvet. I nogle tegne- og billedbehandlingsprogrammer, kan man få oplyst mængden af pixels med en bestemt farve. I dette billede på 250 x 250 pixels dækker den grønne farve 60% af arealet og bilen dermed 40%. Vi mangler et fornuftigt størrelsesforhold for at kunne bruge oplysningen til noget, men lad os antage, at bilen er afbilledet med cirka en ottendel af sin størrelse. Hvis vi ganger højde og bredde med 8 lander vi på 2.000 x 2.000 pixels svarende til 2 meter x 2 meter eller i alt 4 m2, hvoraf bilen udgør 40%, hvilket svarer til 1,6 m2. Nu har vi fundet en metode til at finde bilens tværsnitsareal, så lad os komme tilbage til formlen.
Vi kan jo så bruge oplysningerne til at lave lidt talgymnastik og vise, hvorfor det er så pokers vigtigt at have den rigtige indstilling på front- og hækspoiler.
Vi sætter Cw til 0,4 og tværsnittet til1,6 m2 og får dette resultat:
| Tværsnit |
1,6 |
|
| CW |
0,4 |
| Hastighed |
15 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
| Modstand |
93,6 |
374,4 |
1.497,6 |
3.369,6 |
5.990,4 |
9.360,0 |
13.478,4 |
18.345,6 |
23.961,6 |
30.326,4 |
37.440,0 |
For mere præcist at vise udviklingen i luftmodstanden, så er der her en grafisk fremstilling:
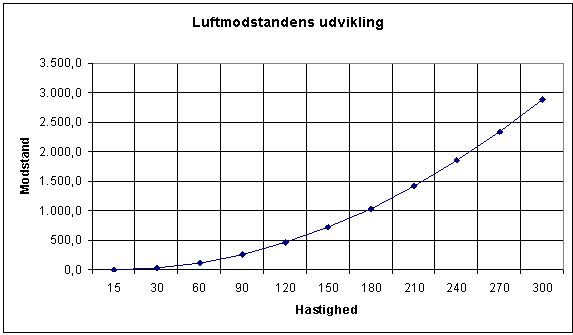
Hvis man kigger på tallene, så holder postulatet om fordobling af hastighed og firedobling af modstand ganske godt.
Det gælder derfor om, at reducere effekten af spoilerne mest muligt i forhold til den downforce der er brug for på den aktuelle bane. Kunne vi reducere Cw til 0,37 ville vi kunne køre en anelse hurtigere og accelerere en anelse hurtigere - og det er marginalerne man kan vinde på!
| Tværsnit |
1,6 |
|
| CW |
0,37 |
| Hastighed |
15 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
| Modstand |
86,6 |
346,3 |
1.385,3 |
3.116,9 |
5.541,1 |
8.658,0 |
12.467,5 |
16.969,7 |
22.164,5 |
28.051,9 |
34.632,0 |
Hvis vores bil nu får en skade under løbet, så påvirker det Cw-værdien negativt. Vi kan ikke sætte et præcist tal på, men lad os antage, at vi mister frontspoileren og får et par buler. Vi sætter Cw til 0,5 (25% forøgelse) og får så dette resultat:
| Tværsnit |
1,6 |
|
| CW |
0,5 |
| Hastighed |
15 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
| Modstand |
117,0 |
468,0 |
1.872,0 |
4.212,0 |
7.488,0 |
11.700,0 |
16.848,0 |
22.932,0 |
29.952,0 |
37.908,0 |
46.800,0 |
Forøgelsen i luftmodstanden skulle gerne være svare til de 25% forøgelse, og det er den da også. Vidste du, at kørsel med et nedrullet vindue kan ændre Cw-værdien med 10-15%? Det vil sige 10-15% lavere topfart eller 10-15% større brændstofforbrug!
En anden ting, vi kan bruge tallene til, er at regne baglæns for at finde bilens hestekræfter. Det er jo desværre sådan, at man i nogle spil ikke oplyser specielt meget omkring bilerne, og det er pokkers svært at vælge den rigtige gearing, når man ikke kender motorens ydelse. Vi vil jo gerne have en tophastighed, som er realistisk i forhold til vores bils formåen, så lad os lege lidt med tallene.
Lad os bruge en teoretisk bil som vejer 1.560 kg, har et tværsnit på 2,15 m2, en Cw på 0,54 og en topfart på 300 km/h.
Vi skal kende bilens rullemodstand eller den friktion som skal overvindes for at bilen begynder at rulle. Det er klart, at underlaget har stor betydning her, så heldigvis har behjertede mennesker lavet fine tabeller, hvor værdierne findes.
Kørebanens belægning |
Koefficient fR |
God asfalt |
0,007 |
Våd asfalt |
0,015 |
God beton |
0,008 |
Ujævn beton |
0,011 |
Stenbro |
0,017 |
Dårlig belægning (ujævn, hullet) |
0,032 |
Jord |
0,15 - 0,94 |
Løst sand |
0,15 - 0,3 |
Disse værdier er tilnærmelsesvise - skulle de være præcise, måtte vi kende dækkets præcise bredde, mønster, mønsterdybde og gummiblandingens blødhed, men til eksemplet her, så går det an.
Formlen for rullemodstand er:
Fr = 9,81 * fR * Gz * cos
a
Fr = Rullemodstand i N (Newton)
fR = Rullemodstandskoefficient
Gz = Samlet totalvægt i kg
cos
a = cosinus til stigningsvinklen i grader (vi sætter den til 1 svarende til vandret)
På god, tør asfalt er rullemodstanden (fR) for en bil på 1.560 kg derfor:
9,81 * 0,007 * 1560 * 1 = 107,13 N
Formlen for luftmodstand kender vi allerede, men her skal vi bruge resultatet i N, så hastigheden skal omregnes til meter per sekund. Det gør man ved at dividere hastigheden km/h med 3,6 (60 sek * 60 min / 1000 meter)
Luftmodstanden (fL) for vores bil bliver så:
0,5 * 0,54 * 2,15 * 1,3 * (300/3,6)ˆ2 = 5240,42 N
Effektbehovet eller den kraft som skal være i motoren for at opnå denne hastighed er dermed:
((fR + fL) * (300 / 3,6 )) / 1000 = 445,61 KW
Det er nu ikke helt korrekt, da der også vil være et krafttab i transmissionslinien. Det kan normalt sættes til 5%, så effektiviteten bliver 95% (0,95) for hver aksel, hvilket i vores tilfælde vil være kardanaksel og bagaksel. Behovet bliver derfor:
(445,61 / 0,95) / 0,95 = 493,75 KW
som omregnes til HK ved at gange med 1,341022 (1 HK er 0,7457 KW) og vores bil skal derfor have
493,75 * 1,341022 = 662,13 HK
ved 8.000 rpm for at kunne køre 300 km/h.
Men det fortæller os jo ikke noget om resten af effektkurven. Hvor ligger den maksimale ydelse? Ud på banen og måle accelerationstider! Med lidt talgymnastik kan man lave en kurve, som kunne komme til at se således ud:
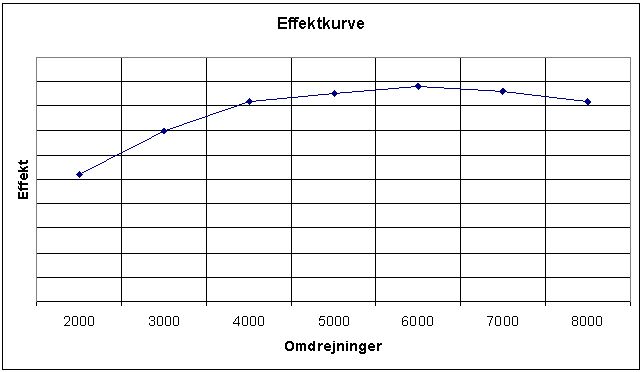
Hver vandret linie er 50 HK og da vi kender værdien ved 8.000 rpm (662 HK) kan vi se, at motoren ved 6.000 rpm yder knap 700 HK. Vi kan også se, at vi vil få det optimale gearskifte ved cirka 7.000 rpm og at motoren helst ikke skal falde mere end 1.000 rpm, når gearet er koblet ind.
Vi skal derfor starte med at vælge en passende gearing til første gear, og hvordan gøres det så? Det vil altid være et kompromis mellem ønsket om maksimal acceleration, banens layout med hensyn til antal sving og hvor skarpe de er, de lige strækninger og deres længde. Et godt sted at starte er det langsomste sving på banen. Skal man helt ned i første gear, så skal omdrejningerne på det sted, hvor man begynder at accelerere ligge tæt på 6.000. Når det er gjort, så er det bare at regne baglæns. Lad os antage, at vi har testet bilen og banen og fundet frem til, at langsomste kurve tages med cirka 123 km/h. Det giver en topfart i gearet på cirka 165 km/h ((123 / 6.000) * 8.000). Vores differentialegearing er 3,800 og dækkets rulleomkreds er 2,1876
Formlen for valg af gearing til 1.gear må derfor blive:
165 |
= |
(0,06 * 8.000 * 2,18758 ) / (3,8 * X) |
165 |
= |
1.050 / 3,8X |
3,8X * 165 |
= |
(1.050 / 3,8X) * 3,8X |
627X |
= |
1.050 |
X |
= |
1,67 |
Vi vil have bilen til at nå 315 km/h på langsiden, så vi skal beregne 6. gear. Vi skifter lige topfarten på 165 ud med 315 og vupti (og vi behøver kun de sidste tre linier, da den første del af ligningen kun udregner en konstant for bilen):
3,8X * 315 |
= |
(1.050 / 3,8X) * 3,8X |
1.197X |
= |
1.050 |
X |
= |
0,88 |
De mellemliggende gear (2. til 5. gear) laves ud fra en simpel beregning, der baserer sig på, at vi fordeler hastighedsforskellen mellem 1. og 6. gear ligeligt.
Det ser således ud:
| 6. gear topfart: |
315 |
1. gear topfart: |
165 |
| Difference: |
150 |
Fordelt på gearskift (der er fem gearskift fra 1. til 6. gear): 30 km/h pr. gear.
Vi sætter det lige ind i en tabel:
1. gear |
2. gear |
3. gear |
4. gear |
5. gear |
6.gear |
3,8X * 165 = 1.050
627X = 1.050
X = 1,67 |
3,8X * 195 =1.050
741X = 1.050
X = 1,42 |
3,8X * 225 =1.050
855X = 1.050
X = 1,23 |
3,8X * 255 =1.050
969X = 1.050
X = 1,08 |
3,8X * 285 =1.050
1.083X = 1.050
X = 0,97 |
3,8X * 315 =1.050
1.197X = 1.050
X = 0,88 |
1,67 |
1,42 |
1,23 |
1,08 |
0,97 |
0,88 |
Nu er det jo ikke en ideel verden, så det ville være mere end heldigt, hvis der fandtes præcis disse udvekslingsforhold til gearkassen, så man bliver nødt til at vælge de værdier, som ligger nærmest. En afvigelse på +- 5% kan accepteres.
Se, det var lige som benløse fugle - det var der jo ingen ben i.
| |